Grade 12 Mathematics Question Papers And Memos 2018 Pdf

MATHEMATICS PAPER 2
GRADE 12
NATIONAL SENIOR CERTIFICATE
JUNE 2018
MEMORANDUM

NOTE:

• If a candidate answers a question TWICE, only mark the FIRST attempt.
• If a candidate has crossed out an attempt of a question and not redone the question, mark the crossed out version.
• Consistent accuracy applies in ALL aspects of the marking guideline.
• Assuming answers/ values in order to solve a problem is NOT acceptable.

GEOMETRY
S	A mark for a correct statement. (A statement mark is independent of a reason.)
R	A mark for a correct reason. (A reason mark may only be awarded if the statement is correct.)
S/R	Award a mark if statement and reason are both correct.

QUESTION 1

1.1	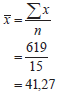Answer only full marks	✓619 ✓41,27 (2)
1.2	σ = 10,63	Answer (2)
1.3	41,27 10,63 41,27 10,63 30,64 51,90 ∴ 8 learners	✓both c.vs ✓ notation ✓ 8 learners (3)
1.4	Q1 29 Q3 49 ∴ Semi - IQR/IKW 49 - 29                             2 = 10	✓ Q1 ✓ Q3 ✓ answer(3)
		[10]

QUESTION 2
2.1	56 + 2 y = 64 2 y = 8 Answer only 1 mark y = 4			✓ correct equation ✓ y-value (2)
2.2	Time (in minutes)	Frequency	Cumulative frequency	✓ 8, 12 and 28 ✓ 43, 60 and 64 (2)
	5 ≤t <10	3	3
	10 ≤ t < 15	5	8
	15 ≤ t < 20	4	12
	20 ≤ t < 25	16	28
	25 ≤ t < 30	15	43
	30 ≤ t < 35	17	60
	35 ≤ t < 40	4	64
2.3		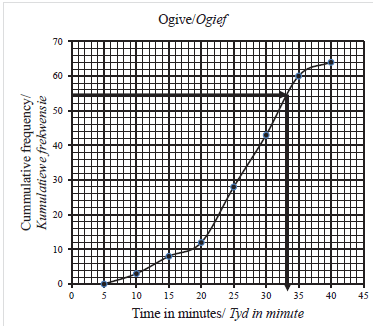		✓ grounding ✓ plotting against the upper limit ✓ shape (3)
2.4	Number of learners= 64 - 54 = 10 Accept[9 -11]			✓ method ✓ 54 ✓ answer (3)
				[10]

QUESTION 3

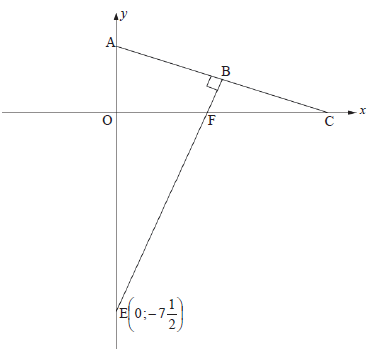3.1	x + py = p y = - x + 1         p ∴ A(0;1)		✓ y-subject of formula ✓ coordinates of A (2)
3.2	OA = 1 ∴ OC = 4(1) = 4 ∴ C (4; 0) mAC =- 1  =1 - 0             p0 - 4 p = 4		✓ OC ✓ - 1 =1 - 0         p 0 - 4 ✓ simplification ✓ p-value (4)
3.3	m EB = 4    EB ⊥ AC y = 4x - 7½		✓ m EB = 4 ✓ equation (2)
3.4	- x + 1 = 4x - 7½   4 -x + 4 = 16x - 30 17x = 34 x = 2 y = ½		✓ equating ✓ simplification ✓ x-value ✓ y-value (4)
3.5	4x - 7½ = 0 4x = 15          2 x =15        8		✓ y = 0 ✓ x-value
3.6		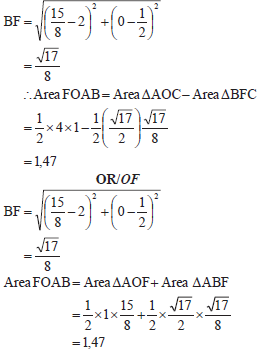	✓ substitution ✓ BF ✓ BC ✓ substitution ✓ answer ✓ substitution ✓ BF ✓ OF ✓ substitution ✓ answer (5)
3.7	r =17      16		✓ answer (1)
3.8			✓ r 2 ✓ equation (2)
			[22]

QUESTION 4

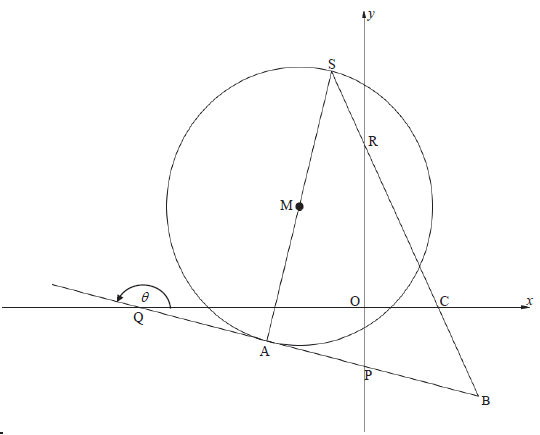4.1	x 2 + 6x + 9 + y 2 - 8 y + 16 = -5 + 9 + 16 (x + 3)2  + (y - 4)2   = 26 ∴ M(- 3; 4)		✓completing the square ✓ x-value ✓ y-value (3)
4.2	r = √26		✓ answer (1)
4.3	m AS = 5    [SA ⊥ QB] y - 4 = 5(x + 3) y = 5x + 19		✓ m AS = 5 ✓ subst.. m AS &(- 3; 4) ✓ equation (3)
4.4	x 2 + 6x + 9 + (5x + 19 - 4)2   = 26 x 2 + 6x + 9 + 25x 2 + 150x + 225 - 26 = 0 26x 2 + 156x + 208 = 0 x 2 + 6x + 8 = 0 (x + 4)(x + 2) = 0 x = -4 or  x s -2 ∴ y = 5(-4) + 19 = -1 Q(- 4; - 1)		✓ substitution ✓ simplification ✓standard form ✓factors ✓ choosing correct ✓ y-value (6)
4.5	-1 = - 1/5 (- 4)+ k ∴ k = - 9/5		✓ substitute (- 4; -1) ✓ answer (2)
4.6	tanθ =- 1/5 ∴ θ = 1690 OQP = 110 [∠s on a str line] ∴ OQP = ORC ∴ RCPQisa cyclic quad [converse∠s same seg]		tanθ =- 1/5 ✓ size of θ ✓ size of OQP ✓ R (4)
			[19]

QUESTION 5

5.1.1		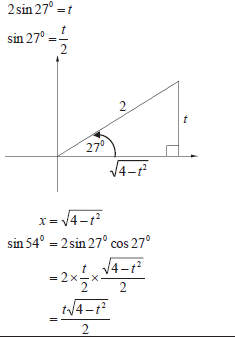✓ sin 270 = t /2 ✓ x =  √4 - t 2 ✓ 2 sin 270 cos 270 ✓ substitution (4)
5.1.2	tan 5130.cos 270 = (- tan 270) cos 270 = - sin 27º .cos 270      cos 270 = - t /2	✓ (- tan 270 ) ✓ - sin 270          cos 270 ✓ - t /2
5.1.3	cos 870 = cos(600 + 270 ) = cos 600.cos 270 - sin 600.sin 270 = ½ . √4 - t 2 - √3 . t /2             2          2 = √4 - t 2 - t 3             4	✓    600 + 270 ✓ expansion ✓subst√ 4 - t 2 & t /2                     2 ✓ subst. ½ &√ 3/2
5.2	sin(- 2a )cos(900 + a ) sin(- a + 3600 ).cos(- a -1800 ) =(- sin 2 a )(- sin a )      (sin a )(- cos a ) = -2 sin a cos a            cos a = -2 sin a	✓ (- sin 2a ) ✓ (- sina ) ✓ sina ✓ (- cosa ) ✓ 2 sina cosa ✓ - 2sina (6)
5.3	9 sin2 x - 4 cos2 x = 0 (3sin x - 2 cos x)(3sin x + 2 cos x) = 0 ∴ 3sin x =± 2 cos x tan x =± 2               3 x = 33, 690 +1800.k orx = 146, 310 +1800.k k ∈Z	✓ factors ✓ both equations ✓ tan x = ± 2                        3 ✓ both 33,690 &146,310 /- 33,690 ✓ 1800.k & k ∈Z(5)
		[22]

QUESTION 6

6.1	Amplitude= 2	✓ answer(1)
6.2	1 ≤y ≤ 5	✓min & max ✓ notation(2)
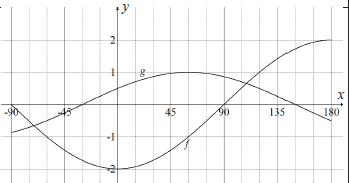
6.3		✓ both x- intercepts - 300 &1500 ✓ max TP & y- intercept ✓ shape (3)
6.4	- 300 < x < 00	✓both c.v.s ✓ notation(2)
6.5	h(x) = sin(x + 900) - 2 = cos x - 2	✓✓ sin(x + 900) - 2 ✓cos x(3)
	[11]

QUESTION 7

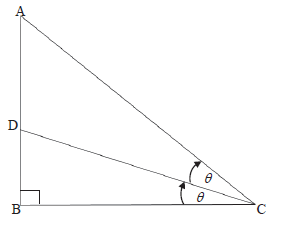
7.1	Aˆ = 900 - 2θ	✓ answer(1)
7.2	sinθ = DB            DC	✓ answer (1)
7.3	DC = DB          sin θ and AD = 2DB = 2DB         DC  = AD  in ΔADC sin(900 - 2θ )    sin θ   DB sin θ =  2DB cos 2θ    sin θ        DB   =2DB sin θ.cos 2θ     sin θ DB.sin θ = 2DB.sin θ.cos 2θ 2 cos 2θ = 1 2 cos 2θ - 1 = 0	✓ AD = 2DB ✓ sine rule ∆ADC ✓ subst. in sine rule ✓ cos2θ ✓ equation (5)
		[7]

QUESTION 8

8.1		Perpendicular to the chord			✓ answer (1)
8.2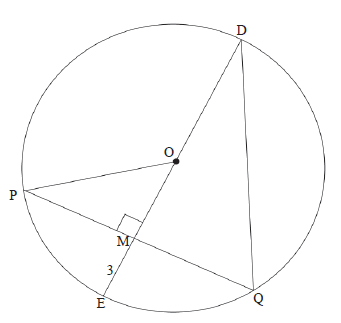
8.2.1	OM = 2x + 3 - 3              2 OR OM =2x - 3              2				✓ answer OR ✓ answer (1)
8.2.2		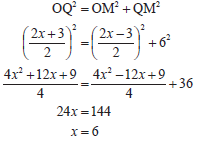			✓ susbt. in Pyth ✓ simplification ✓ standard form linear equation ✓ x-value (4)
8.2.3	DM = 12 DQ = √122 + 62 = √180 = 6√5				✓DM ✓ subst. in Pyth ✓answer (3)
					[9]

QUESTION 9

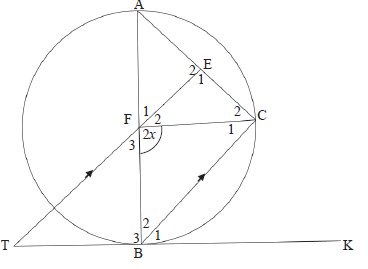
9.1	Aˆ  = x[ ∠ at centre = 2∠at circumf.]				✓S ✓R
	Cˆ 2  = x[ ∠s opp.=sides]				✓S ✓R
	Bˆ1  = x[ tan chord theorem]				✓S ✓R
	Tˆ = x [corresp.∠s, : TF II BC]				✓S ✓R	(8)
9.2	Tˆ  = Aˆ = x ∴ ATBE is a cyclic quad [ converse ∠s same segment]				✓ S ✓ R	(2)
					[10]

QUESTION 10

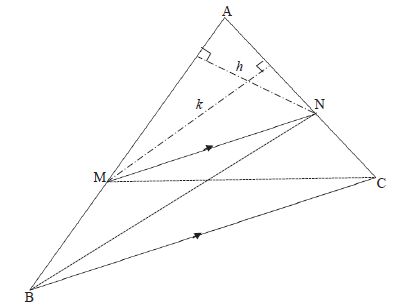
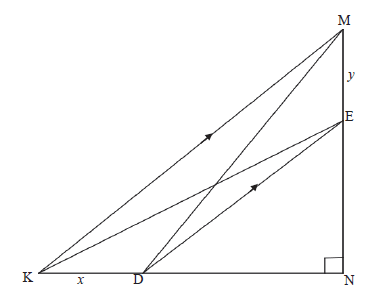
10.1	Contruction:Join BN and height from N ⊥ AM and CM and height from M ⊥ AN Area ΔAMN =½ x AM x h   [same height] Area ΔBMN   ½ x BM x h = AM    BM Area ΔAMN =½ x AN x k   [same height] Area ΔCMN   ½ x NC x k = AN    NC Area ΔBMN Area ΔCMN  [same height, same base MN||BC] = AM = AN    BM    NC	✓constr ✓ S ✓R ✓ S ✓ R (5)
10.2.1	ND = 2 [given]  x 1 ND = 2xand NE =2  [prop theorem DE II KM or] line drawn to oneside of a Δ  y      1 ∴ NE = 2y KM2 = KN2 + MN2 [Pyth theorem] = (3x)2  + (3y)2 = 9x 2 + 9 y 2	✓ S ✓R ✓subst in Pyth theo ✓ simplification(4)
10.2.2	DM2 = DN2 + M N2  [Pyth] = (2x)2 + (3y)2 KE2 = KN2 + NE2   [Pyth] = (3x)2 + (2 y)2 DM2 + KE2 = 4x 2 + 9 y 2 + 9x 2 + 4 y 2 = 13(x 2 + y 2 ) DM2 + KE 2 =13(x 2 + y 2 )     KM2            9(x 2 + y 2 ) =13     9	✓ subst in Pyth ✓ subst in Pyth ✓ value of DM2 + KE2  13(x 2 + y 2 )  9(x 2 + y 2 ) ✓ (4)
		[13]

QUESTION11

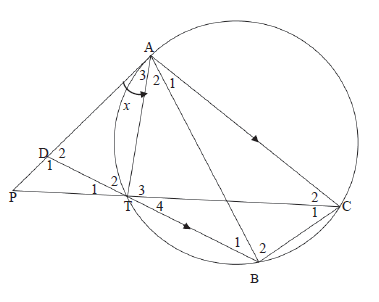
11.1	A1 = B1 [alt ∠s, AC II DB] A3 = B1 [tan chord] ∴ A1 = A3 T2= ACB [ext ∠of a cyclic quad] D2 = B2 [3rd ∠s]		✓S/R ✓S✓R ✓S✓R ✓S
	OR A1  = B1 [alt 3s, AC || DB] A3  = B1 [tan chord] ∴ A1  = A3 T2  = ACB [ext ∠of a cyclic quad] ∴ ΔABC|||ΔADT [∠∠∠]		OR ✓ S/R ✓S ✓S ✓R ✓R ✓R (6)
11.2	Tˆ4  = Tˆ1           [vert opp∠s] Aˆ1  = Tˆ4      [∠sin same seg] A1 = Aˆ3       [proven] ∴ T1  = A3 ∴ PT is a tangent to circle ADT[converse tan chord]		✓S/R ✓ S   ✓R ✓R (4)
11.3	Aˆ3  = Tˆ1     [proven] Pˆ = Pˆ    [common] PTA = Dˆ1  [3rd ∠s] Δ APT|||Δ TPD   [∠∠∠]		✓S ✓S ✓R
	OR Aˆ3 = Tˆ1  [proven] Pˆ= Pˆ    [common] PTA = D1 [3rd ∠s]		✓S ✓S ✓S (3)
11.4	AP = PT       [||| Δs] TP    PD AP.PD = PT2 AP(AP - AD) = PT2 AP(AP -2/3AP) = PT2 AP. AP = PT2        3 AP2 = 3PT2		✓ S/R ✓ simplification ✓ PD i.t.o AP and AD ✓subst in AD (4)
			[17]

TOTAL:150

Grade 12 Mathematics Question Papers And Memos 2018 Pdf

Source: https://www.elimuza.com/grade-12/item/987-grade-12-mathematics-paper-2-memorandum

Posted by: powellagar1989.blogspot.com

Share this post